PROBABILIDADE

DISTRIBUIÇÃO BINOMIAL

· Produção: Laboratório de Bioinformática · Aplicativo suporte: Programa GBOL – Genética Básica on line · Comunidade (facebook): GbolNews

---

Tópicos

Probabilidade

Propriedades

Leis de Probabilidade

Distribuição Binomial

Distribuição Multinomial

Retorna ao GBOL

PROBABILIDADE


Dado um acontecimento A, sendo nA o número de casos favoráveis relativos à sua realização e ñA o número de casos contrários, a probabilidade de A pode ser definida como:

p(A) = nA/(nA + ñA)

De outra forma, a probabilidade é a razão entre o número de maneiras igualmente provável de um evento ocorrer e o número igualmente provável de todos os acontecimentos ocorrerem.

Volta


PROPRIEDADES


O cálculo da probabilidade de um evento A deve satisfazer as seguintes propriedades:

a) 0 £ P(A) £ 1

b) P(S) = 1, sendo S o conjunto de todos os resultados possíveis ou universo.

c) P( ) = 0

Como ilustração, é considerada a cor dos olhos na espécie humana, em que a condição A- determina olhos castanhos e aa, olhos azuis. Do casamento entre genitores heterozigotos (Aa x Aa), formam-se:

Fenótipo	Descrição	Probabilidade
Meninos de olhos castanhos	XY A-	P(XY) P(A-) = ½ x ¾ = 3/8
Meninos de olhos azuis	XY aa	P(XY) P(aa) = ½ x ¼ = 1/8
Meninas de olhos castanhos	XX A-	P(XX) P(A-) = ½ x ¾ = 3/8
Meninas de olhos azuis	XX aa	P(XX) P(aa) = ½ x ¼ = 1/8

Volta


LEIS DE PROBABILIDADE

Lei da soma para eventos mutuamente exclusivos

Eventos mutuamente exclusivos são aqueles cuja ocorrência de um elimina a possibilidade de ocorrência do outro. Nesse caso, a probabilidade de ocorrência de um ou outro evento é expressa por:

P(A ou B) = P(A) + P(B)

Exemplo: No casamento especificado, será estimada a probabilidade de nascer um menino de olhos castanhos ou uma menina de olhos azuis. Assim, tem-se:

P(A) = P(menino de olhos castanhos) = 3/8

P(B) = P(meninas de olhos azuis) = 1/8

P(A ou B) = P(A) + P(B)= 3/8 + 1/8 = 1/4

Lei da soma para eventos não mutuamente exclusivos

Nesse caso, pode-se definir a seguinte expressão de probabilidade :

P(A ou B) = P(A) + P(B) - P(A e B)

Exemplo: No casamento especificado, será estimada a probabilidade de nascer um menino ou uma criança de olhos azuis. Assim, tem-se:

P(A) = P(menino) = 1/2

P(B) = P(olhos azuis) = 1/4

P(A e B) = P(meninos de olhos azuis) = 1/8

P(A ou B) = P(A) + P(B ) - P(A e B) = 1/2 + 1/4 - 1/8

A necessidade de subtrair a probabilidade de meninos de olhos azuis na P(A ou B) pode ser constatada, pois tanto o valor P(menino) quanto P(olhos azuis) inclui a possibilidade de sair menino de olhos azuis. Conseqüentemente, essa probabilidade estaria sendo somada duas vezes, caso não houvesse aquela subtração.

Lei do produto para eventos independentes

Dois eventos são independentes quando a probabilidade de ocorrer B não é condicional à ocorrência de A. A expressão que define a lei do produto para eventos independentes é a seguinte:

P(A e B) = P(A) . P(B)

Exemplo: Em uma família será estimada a probabilidade de nascer menino e ter olhos azuis.

P(menino e olhos azuis) = P(menino) . P(olhos azuis) =(1/2)(1/4) = 1/8

Lei do produto para eventos dependentes (ou condicionais ou ligados)

Nesse caso, tem-se a seguinte expressão de probabilidade:

P(A e B) = P(A) . P(B/A) = P(B) . (P(A/B)

Será considerado agora o gene que deteramina o daltonismo na espécie humana. Trata-se de um gene ligado ao sexo, em que:

Mulheres normais: X^D X^D ou X^D X^d

Mulheres daltônicas: X^d X^d

Homens normais: X^DY

Homens daltônicos: X^dY

Considerando o casamento entre uma mulher normal, portadora, e um homem normal, têm-se as descendências:

Gametas	XD	Y
X^D	X^D X^D	X^D Y
X^d	X^D X^d	X^d Y

Conclui-se que:

P(menino) = P(menina) = ½

P(Normal) = ¾

P(Daltonismo) = ¼

Exemplo: No casamento especificado, será estimada a probabilidade de nascer uma menina daltônica. Verifica-se, nesse caso, que:

P(menina daltônica) ¹ P(menina) x P(daltônica)

Ao contrário, tem-se:

P(menina daltônica) = P(menina) x P(daltonica/menina) = ½ x 0 = 0

Volta


DISTRIBUIÇÃO BINOMIAL

Utilização

A distribuição poderá ser empregada na determinação da probabilidade quando, no evento especificado, se deseja calcular a probabilidade de um acontecimento composto estabelecido por vários eventos. Nesse caso, os eventos que constituem o acontecimento devem ser independentes e a ordem dos eventos, dentro do acontecimento, não influencia o cálculo da probabilidade. Em muitas outras situações, é necessária a reposição dos dados, para que se possa usar a distribuição binomial ou multinomial.

Conceito

Entende-se por distribuição binomial aquela em que os termos da expansão do binômio (ou multinômio) correspondem às probabilidades de todos os eventos possíveis do espaço amostral. O binômio (ou multinômio) é formado pelas probabilidades de cada acontecimento elevadas ao número total de ocorrências.

Ilustração

Para exemplificar, será utilizado o exemplo dos bovinos, considerando três nascimentos. A probabilidade de sair um animal sem chifre é igual a S (S = ¾) e a probabilidade de sair com chifre igual a C (C = ¼). Assim, têm-se as seguintes situações:

Acontecimentos	1^o. Animal	2^o. Animal	3^o.Animal	Probabilidade
3 Com chifres	Com	Com	Com	C³
	Com	Com	Sem
2 Com e 1 Sem chifres	Com	Sem	Com	3C²S
	Sem	Com	Com
	Com	Sem	Sem
1 Com e 2 Sem chifres	Sem	Com	Sem	3CS²
	Sem	Sem	Com
3 Sem chifres	Sem	Sem	Sem	S³

A seqüência C³ + 3C²S + 3CS² + S³ tem dois significados:

a) Cada elemento corresponde a uma probabilidade de um evento do espaço amostral. Sendo probabilidade, verifica-se:

C³ + 3C²S + 3CS² + S³ = 1

b) Corresponde à expansão do binômio:

(C + S)³ = C³ + 3C²S + 3CS² + S³ = 1

Volta


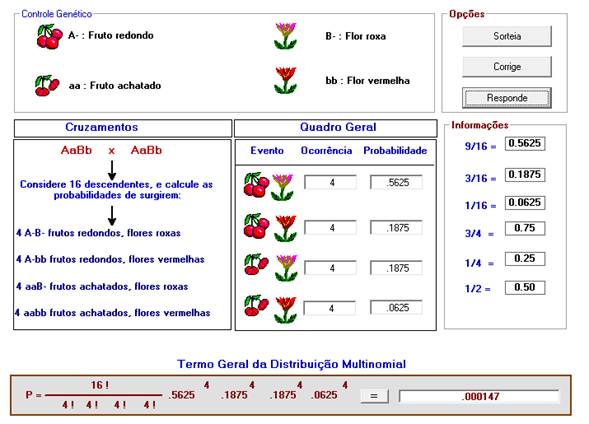
DISTRIBUIÇÃO MULTINOMIAL

A obtenção da probabilidade através da expansão do binômio apresenta inconvenientes quando o valor de n (número total de ocorrências) é relativamente grande.

A expansão do binômio resultará em n + 1 termos e, conseqüentemente, é impraticável obtê-los para n relativamente grande. Adicionalmente, para se obter a probabilidade de um evento, é necessário conhecer a probabilidade de todos os outros que constituem o espaço amostral. Outro aspecto de dificuldade ocorre quando se têm vários eventos, estabelecendo-se, portanto, um multinômio.

Para contornar os problemas, podem-se estimar as probabilidades, utilizando-se o termo geral da distribuição multinomial. Esse procedimento é mais adequado, pois permite estimar a probabilidade do evento desejado sem ser necessário conhecer qualquer outro termo do multinômio.

O termo geral é expresso por:

P(E) =[ N!/(n₁! n₂! ... n_n!)] p₁ⁿ¹ p₂ ⁿ² ...p_n ⁿⁿ

em que

n_i = número de ocorrências do evento i

N = número total de ocorrências

p_i = probabilidade de ocorrência do evento i

Exemplo 1. Probabilidade de surgirem 4 meninos e 2 meninas

Exemplo 2:

Volta